- 3장: 종속변수 Y가 수치형데이터 일때 이를 예측하기 위해 최소제곱법을 사용하는 선형회귀를 다룸
- 4장: 종속변수 Y가 범주형데이터인 경우를 다룸
⇒ Y가 양적,질적도 아닌경우는? 선형회귀나 분류 사용 ❌
4.6.1 Linear Regression on the Bikeshare Data
https://www.kaggle.com/c/bike-sharing-demand/
이 데이터의 종속변수는 'bikers'로, 워싱턴 DC의 자전거 공유 프로그램의 시간당 이용자 수
⇒ 질적 변수도, 양적 데이터도 아니다. 0이상의 정수값, 즉 '건수(count)'를 나타낸다
<설명변수>
변수 설명
| mnth | 월, 1년 중 몇 월인지 |
| hr | 시간, 0-23시 |
| workingday | 평일 여부를 나타내는 지시변수로, 주말이나 공휴일이 아니면 1 |
| temp | 섭씨 온도를 정규화한 값 |
| weathersit | 날씨 상태를 나타내는 질적 변수로 4가지 값을 가짐: 맑음, 안개/흐림, 약한 비/눈, 강한 비/눈 |

표 4.10 선형회귀를 사용하여 예측한 자전거 이용자 수
(-12.89라는 계수는 자전거 이용자가 평균적으로 12.89 감소한다 의미)
a. 날씨가 맑음에서 흐림으로 변할 때 시간당 평균 12.89명의 이용자가 감소한다.
b. 날씨가 더 나빠져서 비나 눈이 올 경우 추가로 53.60명이 더 감소한다

선형 회귀 모델에는 몇 가지 문제점이 있음.
- 음수 예측값 문제:
- 전체 예측값의 9.6%가 음수로 나옴
- 자전거 이용자 수가 음수일 수 없으므로 이는 현실적이지 않은 결과
- 분산의 불균일성(heteroscedasticity) 문제:
- 이용자 수가 적을 때는 분산도 작아야 하는데, 데이터가 이를 보여줌
- 예시:
- 겨울철 새벽 1-4시, 비 올 때: 평균 5.05명, 표준편차 3.73
- 봄철 출근시간 7-10시, 맑을 때: 평균 243.59명, 표준편차 131.7
- 이는 선형 회귀의 기본 가정(오차항의 분산이 일정)을 위배 (모든 구간에서 변동성이 비슷해야 한다)
2.정수값 응답변수 문제:
- 자전거 이용자 수는 정수값이어야 함
- 하지만 선형 회귀는 연속적인 값을 예측
선형 회귀는 2.5명이나 3.7명 같은 예측값을 만들 수 있는데, 실제로는 자전거 이용자 수가 2.5명이 될 수는 없습니다. 이는 모델이 현실을 정확히 반영하지 못한다는 것을 의미
로그 변환 접근법

장점:
- 음수 예측값이 나올 수 없음 (로그 값의 지수를 취하면 항상 양수)
- 원본 데이터에서 보였던 분산의 불균일성 문제가 많이 해결됨 (4.14 오른쪽 그림)
단점 :
- 응답변수가 0인 경우에는 로그 변환을 적용할 수 없음
- 자전거 이용자가 전혀 없는 시간대의 데이터를 처리할 수 없다는 문제 발생
- 설명변수 Xj가 한 단위 증가하면 Y의 로그 평균이 βj만큼 증가한다"라는 식의 해석은 직관적이지 않음
4.6.2 Poisson Regression on the Bikeshare Data
선형 회귀의 한계를 극복할 수 있는 포아송 회귀 존재
포아송 분포
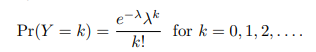
- λ: 평균값 E(Y)
- k: 발생 횟수
- k!: k의 계승(팩토리얼)
Y는 음이 아닌 정수값만 가짐 (0, 1, 2, ...)
평균(λ)과 분산이 같음
- λ = E(Y) = Var(Y) ⇒ 평균이 클수록 분산도 커짐 </aside>
Y는 음이 아닌 정수값만 가짐 (0, 1, 2, ...)
평균(λ)과 분산이 같음
- λ = E(Y) = Var(Y) ⇒ 평균이 클수록 분산도 커짐
포아송 분포는 개수(counts)를 모델링 하는데 사용
Bikeshare 데이터 적용 예시
단순 예시 (λ = 5인 경우):
- 0명 이용: 0.67% 확률
- 1명 이용: 3.4% 확률
- 2명 이용: 8.4% 확률
현실에서는 자전거 공유 프로그램의 평균 이용자 수 λ = E(Y)가 하루 중의 시간, 연중 월, 날씨 조건 등의 함수로 변할 것
따라서 자전거 이용자 수 Y를 λ = 5와 같은 고정된 평균값을 가진 포아송 분포로 모델링하는 대신, 평균이 공변량의 함수로 변할 수 있게해야한다.
포아송 회귀 모델의 수식

log(λ) = β₀ + β₁X₁ + ... + βₚXₚ 형태로 모델링하면 λ = exp(β₀ + β₁X₁ + ... + βₚXₚ)가 된다.지수함수(exp)는 항상 양수값을 출력하므로 예측값 λ가 항상 양수가 됨을 보장함
(자전거 대여 수는 음수가 될 수 없으므로 이는 중요한 특성임)
ex) 날씨가 맑음(X₁=0) ⇒ 흐림(X₁=1)으로 바뀔 때
- λ₂ = λ₁ × exp(β₁)
즉, 원래 평균에서 exp(β₁)배만큼 곱해져서 변화합니다
이는 항상 양수이며, 현실적인 해석이 가능
선형 회귀와의 주요 차이점
- 변화를 배수로 해석
- 포아송: 항상 양수 예측 / 선형: 음수 예측 가능성 있음
- 포아송: 평균=분산 / 선형: 일정한 분산
선형회귀: 자전거 이용량이 100명이든 1000명이든 분산은 똑같음
⇒ 현실적 x, 보통 이용량이 많을 때 변동성도 더 큼
포아송 회귀: 평균 = 분산 (mean = variance) 가정
평균 이용량이 100명이면 분산도 100
평균 이용량이 1000명이면 분산도 1000
포아송 회귀 후 결과 분석


봄과 가을에 이용률이 가장 높고 출퇴근 시간대에 이용률이 피크를 보임
4.6.3 Generalized Linear Models in Greater Generality
세 가지 회귀 모델(선형,로지스틱, 포아송) 의 공통점
- 각각 예측변수 X₁, ..., Xₚ를 사용해 반응변수 Y를 예측한다.
- 선형회귀: Y는 가우시안/정규분포
- 로지스틱 회귀: Y는 베르누이 분포
- 포아송 회귀: Y는 포아송 분포
- 각각 Y의 평균을 예측변수의 함수로 모델링한다.
- 선형회귀

- 로지스틱 회귀

- 포아송 회귀

3.링크함수
- 선형회귀: η(μ) = μ
- 로지스틱 회귀: η(μ) = log(μ/(1-μ))
- 포아송 회귀: η(μ) = log(μ)
가우시안, 베르누이, 포아송 분포는 모두 지수족이라고 알려진 더 넓은 분포족의 일부
다른 잘 알려진 구성원으로는 지수분포, 감마분포, 음이항분포가 있다.
이런 모델들을 일반화 선형 모델(GLM)이라고 함
'📒base > ISL' 카테고리의 다른 글
| [ISL] 6.1 Subset Selection (0) | 2024.11.27 |
|---|---|
| [ISL] 4.4.3-4.4.4 QDA, Naive Bayes (0) | 2024.11.22 |
| [ISL] 4. Classification (1) | 2024.11.01 |
